cellular automata
I've spent a month or so investigating emergence. I think that all this is required for artificial life to emerge is the right sort of complex system. The Earth is great but there are likely much simpler systems that life can emerge from.
One good candidate is cellular automata. I loved playing around with Conway's Game of Life as a kid. It's a simple ruleset that leads to incredible complexity. If you haven't come across it before, I recommend skimming the wikipedia page. It has some cool mathematical properties and people have made incredible things with it, such as a prime number generator and even a digital clock!
The game of life is just the start though, there are endless possible cellular automata and the right combination of rules could lead to even greater complexity. I made a little java program to play around with emergence and CA. It has configurable tile types, many ways of generating random rulesets and altering/combining them.
An example rule generator is: Each tile can be in one of N different states. Each 'turn', the cell adds up all the states that surround it (the state's value is 0-N). Based on this total, generate the next state using some algorithm. The upside of this weird system is that I can now add some constant to this total and have endless variations instead of a single rule.
Most of these random rules produce rubbish. Some just decay to a single colour very quickly. Some are too chaotic like tv static.
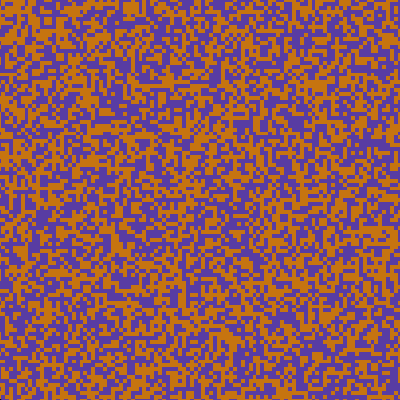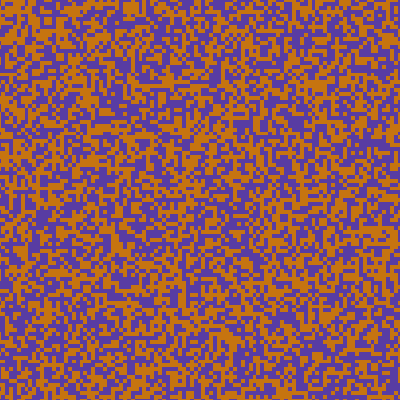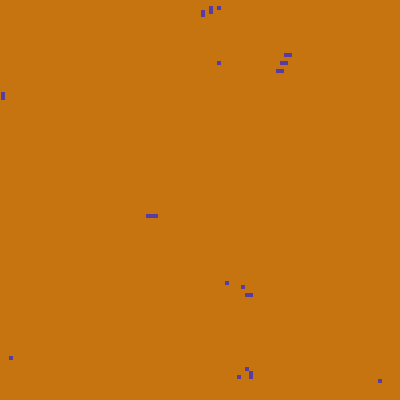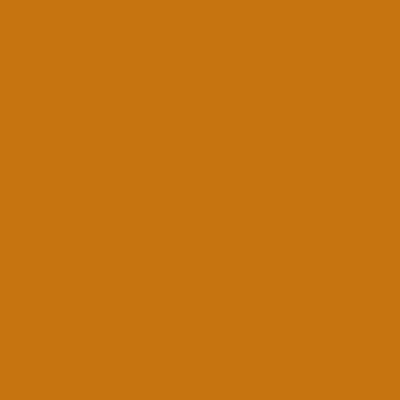

crystallization
One thing I see a lot is what I like to call crystallization. If there exists a stable arrangement of cells and it's possible for it to appear, it will remain and likely grow.
An interesting parallel to real life is grain boundaries appearing. This is very common for certain rule generators and is caused by two areas of crystallization starting in different places with offset patterns. When they meet, they aren't able to merge and remain stable with a boundary line between them.
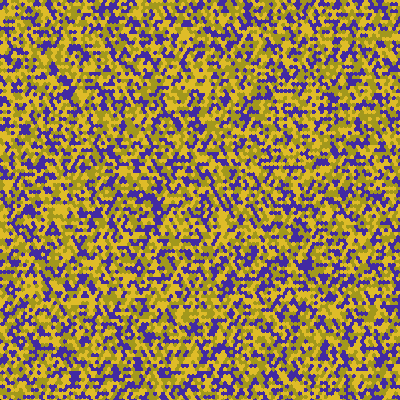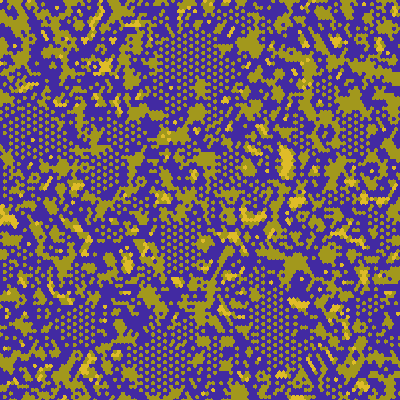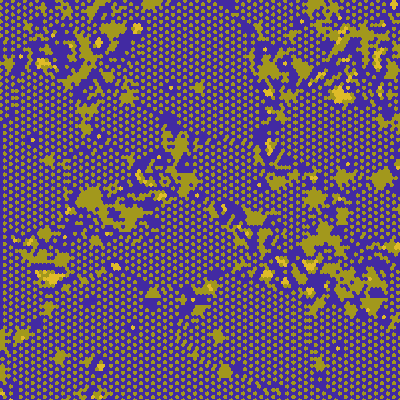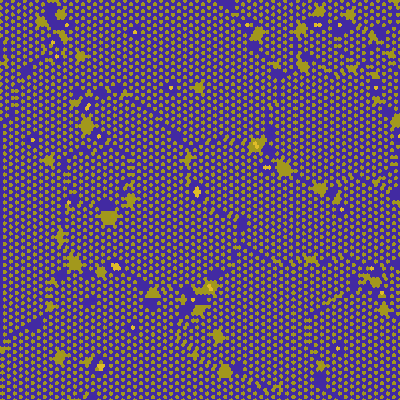
enzymes
This one may be a bit of a stretch but I like the analogy. In the game of life, there are glider guns. A glider is a stable but moving arrangement. There are larger stable structures that create these gliders, firing off gliders at a constant rate forever. I think of this as an enzyme, the larger structure creates these gliders without being used up itself.
One of my rule generators often makes complex systems of these enzymes which consistently emerge from a random grid.
My favourite rules I've discovered are similar to these. Many enzymes but also a structural element to it which these enzymes can modify, leading to constantly shifting corridors. The generator for this creates many similar rulesets and I've spent hours staring at them.

other bits
-
The grids I'm using wrap around, which means all this is technically happening on the surface of a torus
-
In order to get interesting complexity instead of chaos, it's a good idea to constrain what each tile 'knows' about. The best rulesets I've found are ones where each tile only looks at 2-4 of its neighbours instead of all of them.
-
I couldn't find a good way to automatically-detect interesting rules, I ended up looking at a huge grid of different rules and regenerating them if they weren't instantly interesting.
-
Fractals keep popping up in the interesting rules. Often if I clear the grid and set a single tile to a different state, it will create a fractal pattern.


- I'm not sharing the application because the code and UI are a bit messy.
credits
Special thanks to tommyettinger for identifying that I was looking for a unary hash and sharing one that he created, and to this comment by Kenneth Shaw for the branchless pixel to hex algorithm I used in my rendering shader.
what next?
I haven't managed to create life, sadly. I had hoped that combining these rules in one larger area would lead to even more complexity but that just gets too chaotic. I think CA have some limitations; it's very difficult for structures to move, and if they do it's very difficult for them to stop or move in a different direction. I do still think it's possible to create life in CA but I don't think it's the easiest way. I have some ideas for other types of systems that could be more fruitful, in the future I hope to try some of them.
One thing I'm very excited about is looking up what others have done with CA and artifical life. I've purposefully avoided looking into what others have done because I love to find my own path. It also gives me greater appreciation for what others have achieved. Maybe next week's post will be an overview of the research other have done.
comments