chaos

Chaos theory has been on my mind a lot recently. I like Lorenz's definition 'Chaos: When the present determines the future, but the approximate present does not approximately determine the future'.

I wanted to play around the the classic chaos theory model, the double-pendulum. I started to model it with a physics engine but that didn't seem like the best way to go about it. Luckily you can simulate it purely with a few equations, so I converted some code from a web demonstration (thanks micael).

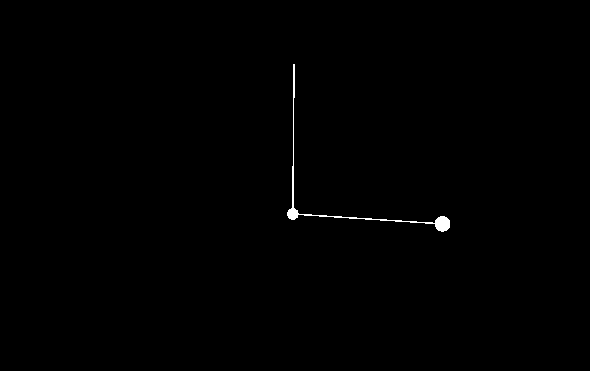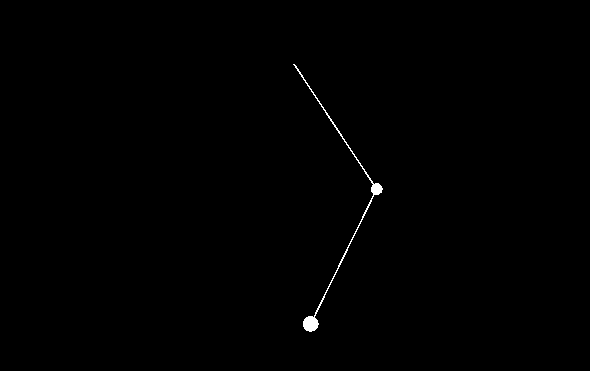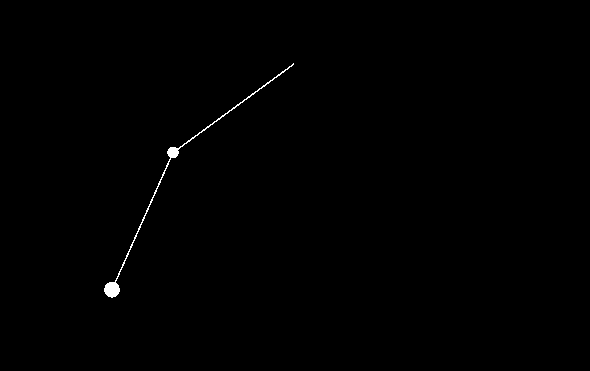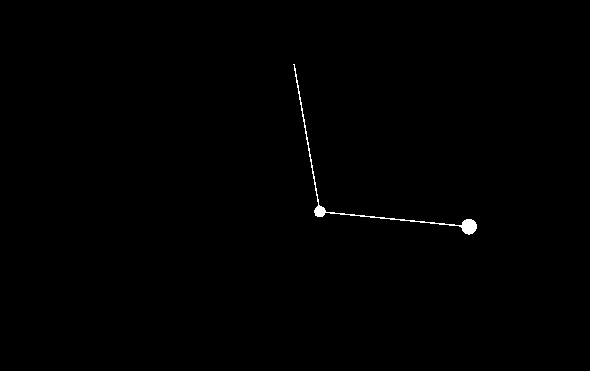
My first test was to try lots of similar initial conditions to see how long it takes for them to diverge. The closer the initial conditions the longer it takes, which is logical.

I needed another way to visualise it instead of a mess of lines and circles. I simulated a double-pendulum for each pixel, with the starting condition altered slightly based on the x and y position of the pixel. Then I pick some characteristic about the system, like the difference between the angles, and used that to determine the brightness of the pixel. Then I let all the simulations run and turned it into an image.

As you can see, I had a lot of fun with this. It seems to be a good source of fractal-like forms. I was curious if anyone else had tried something similar found that Jeremy Heyl created this lovely image using a similar technique to mine.

If the double-pendulum can be abstracted down to a few equations, it should be possible to create some chaotic system of equations that does not describe a real physical phenomenon. I tested out some random rubbish formulas, just a few trigonometric functions with 3 variables, and got some fun results.

If you're interested in chaos theory, I highly recommend checking out this blog and the program made by the author. I'm probably going to write more about this at some point as this guy is a major inspiration to me.

attributions

Jeremy Heyl's pendulum image licensed under cc3.0

comments